The Great British Summer - cool and showery, now’t on telly, rusting barbecues, light nights, idle scopes, humid days, lobster people and thundery downpours... and more light nights. From the latitude of ‘god’s own country’ astronomical twilight is actually absent for 82 nights over the summer and only the brighter stars are readily visible before 11pm. Indeed, for a fortnight either side of the summer solstice many of the fainter stars normally visible, are so for only a few hours, if at all. Bright or faint, stellar brightness is quantified in different ways.
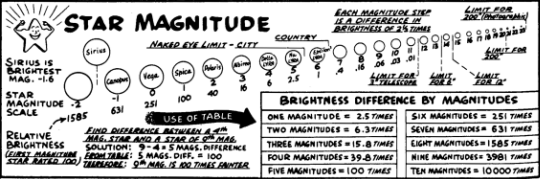
I trust even the most casual of observers notice that to the naked eye not all stars are alike–either in brightness or colour. The brightness of any celestial object is expressed in terms of magnitude, a classification system that can be traced back to the 1st century AD to the great astronomer Ptolemy and then revised by Hipparchus a century later into six classes of brightness. Our present day system was formalised in 1860, when the Astronomical Union decided that a half-pound plumbers candle seen from a distance of 1 mile was found to be equivalent in brightness to many of the brighter stars visible. Hence such stars were considered to be of the first magnitude.
The scale of stellar brightness works in similar fashion to that of a golfer’s handicap, with the most brilliant performers having the lowest values. Each magnitude class is separated by a factor of 2.5 orders e.g. a second magnitude star is 2.5 times fainter than a first magnitude star. A third magnitude stars is 2.5 times fainter than a second magnitude star and so on. A star of sixth magnitude, the generally accepted naked eye limit from dark rural sites, is thus 100 times fainter than a star of the 1st magnitude.
The most brilliant stars visible have an apparent brightness expressed in negative terms. Two may be seen from the UK; Sirius, the brightest star in the night sky (now set) and Arcturus (-0.04), which is located high to the SE as darkness falls. By convention there are 21 stars of the first magnitude in the heavens ranging from Sirius, Mag -1.46 to Regulus +1.35. Stars from +1.5 to +2.5 are counted as second magnitude stars, 2.5 to 2.5 as third magnitude, and so on. Of the 21 brightest stars ranged across the heavens, 15 are visible from the UK at some time during the year.
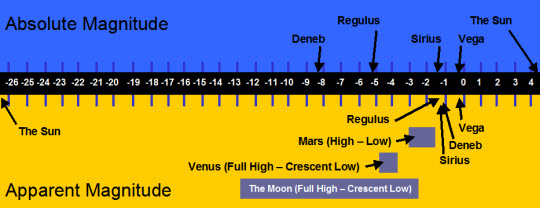
Absolute v. Apparent Magnitude of selected stars, planets and the Moon. (Planets
only have an Apparent Magnitude, varying with crescent and our varying distance from them.)
The same magnitude system also applies to other celestial bodies. Venus, which was so dominant over the winter, can attain Mag - 4.6. Jupiter regularly reaches Mag -2.5, as too can Mars on rare occasions. A full moon reflects sunlight equivalent to Mag -13, whilst the Sun baths our world in ‘factor’ –27, that’s 400,000 times brighter than a full moon or 10 billion times brighter than Sirius!

Stars in the Constellaton Canis Major: Sirius
is giant in appearance but a baby in practice.
Image Credit: SkyAndTelescope.com
Apparent magnitude only tells part of the story; astronomers regard the measurement of Absolute Magnitude as far more informative about what a star is really like. It is human nature to perceive the celestial dome as a two dimensional canvas and we often fail to appreciate that stars are scattered throughout space at hugely varying distances and luminosities.
Apparent brightness is just that – apparent – and bears no relation to true luminosity. A star may appear bright by virtue of being situated relatively nearby, whereas visually fainter, more distant stars may in comparison be considerably more luminous. In an effort to make scientific sense of all this, astronomers use an Absolute Magnitude scale to gauge the real luminosity of any star. This assumes a standard distance for all stars equivalent to10 parsecs or 32.6 light years. One parsec (Named from an abbreviation of the parallax of one arc second ) is the distance at which one astronomical unit (AU, the distance from the Earth to the Sun) subtends an angle of one arc second. A parsec is equal to about 3.26 light-years (31 trillion kilometers or 19 trillion miles) in length.
Using this method our own brilliant Sun would have an absolute magnitude of +4.2, not so brilliant after all, hardly noticeable in a sky adorned with sparkling luminaries. On the other hand our pole star – Polaris, which is of second magnitude, would appear to rival Venus (mag -4.4) if located at 10 parsecs.
A few of our brighter summer luminaries: Vega, Capella and Arcturus would still appear similar in brilliance, others would most definitely not. Some stars are ‘born special’ and are really luminous. Deneb for instance, in the constellation of Cygnus is an extreme example of this scenario. Visually, Deneb makes it into the stellar top 20 and yet it is far more remote than the majority of brighter stars visible. If Deneb were situated just 10 parsecs away it would blaze forth at Mag -8, twice as bright as Venus appears. Casual stargazers might marvel at Alpha Cygni, but seasoned astronomers, especially from these latitudes where Deneb is visible all year round, would soon tire of its radiance, severely restricting deep sky observations.
This begs the question, what would astronomers in the close proximity of such a brilliant luminary make of their cosmos? Perhaps on reflection our Sun and this planet are ideally placed to study and appreciate the boundless universe and marvel at the magnitude of it all!
- Log in to post comments